Rotation and Reflection

Rotational Symmetry 

. If an object can be rotated from the centre and look the same in under 360°

Order of symmetry 

. How many times an object can be rotated and look the same after 360°

Finding Rotational Symmetry:

1. Trace the image and turn it, if it looks the same in under 360°, it has rotational symmetry
2. Count how many times the object looks the same after 360°

Example:

Q) Workout if the shape has rotational symmetry. If so, what is the order of symmetry?

1. The shape has rotational symmetry because after 72° the shape looks like it did at the start
2. Order symmetry is 5 → at 72°, 144°, 216° and 288° and 360°

A) Yes and 5

Tips:

. An easier way to workout order of symmetry is to find angle of the first order

. e.g 72° and divide by 360° → 360 ÷ 72 = 5

Reflection:

. A reflected image is the image that appears on the opposite side of the mirror line

1. Find how far, from a point on the mirror line, what each corner of the shape is
2. Draw the shape onto the other side

Example: 

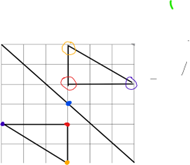
Q) Draw the reflection of the shape

Use a point on the mirror line e.g the blue dot → start by finding one corner, e.g the one circled in red

. This is one square up from the blue point so when it is reflected do the opposite and go one square down from the same point

. The corner circled in orange is three squares up from the blue dot, so the reflection is three squares down

. The corner circled in purple is one square up and three squares right form the blue dot, so the reflection is one square down and three squares left