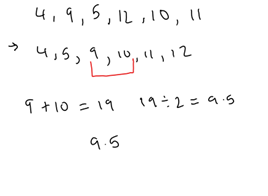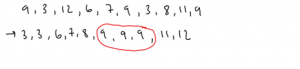Data Handling – Averages

Median – the middle number when all the numbers are arranged from smallest to biggest

Example:

Q) Find the median in this set of numbers: 4, 9, 5, 12, 10, 11

1. Arrange the numbers smallest to biggest
2. The two numbers that lie in the middle are 9 and 10. Add both middle numbers and divide the answer by 2 to find the middle value 9 + 10 = 19 2 = 9.5

A) 9.5

Tips:

. When there is a odd number of values in the set, the median is easier to find as it is just the middle number no further calculation needs to be done

Mode – most common number in the set 

Example:

Q) Find the mode from in this set of numbers: 9, 3, 12, 6, 7, 9, 3, 8, 11, 9

1. Arrange the numbers from smallest to biggest
2. Find the number that occurs the most 

A) 9

Range – the difference between the largest and smallest value from the set

Example: 

Q) Find the range in this set of numbers: 22, 72, 54, 95, 23, 45

1. Arrange the numbers in order from smallest to biggest
2. 95 (largest) – 22 (smallest) = 73

A) 73

Tips:

. Range gives an idea of how the data is spread

Mean – also known as average, can be found by adding all the values in the set and divide by how many numbers there is

Example:

Q) Work out the mean in this set of numbers: 22, 5, 87, 20, 35, 65, 47, 3

1. Add all the values 22 + 5 + 87 + 20 + 35 + 65 + 47 + 3 = 284
2. There are 8 numbers in the set → 284 ÷ 8 = 35.5

A) 35.5

Averages From Bar Charts:

Example:

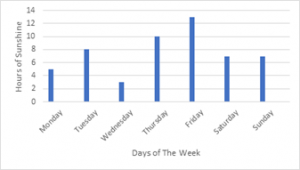
Q) 1) Which day was least sunny? 2) What is the modal number of hours of sunshine? 3) What is the range of hours of sunshine?

1. Wednesday (3 hours)
2. 7 hours (saturday and sunday)
3. Friday most hours of sunshine (13 hours) and Wednesday least hours of sunshine (3 hours):  13 – 3 = 10